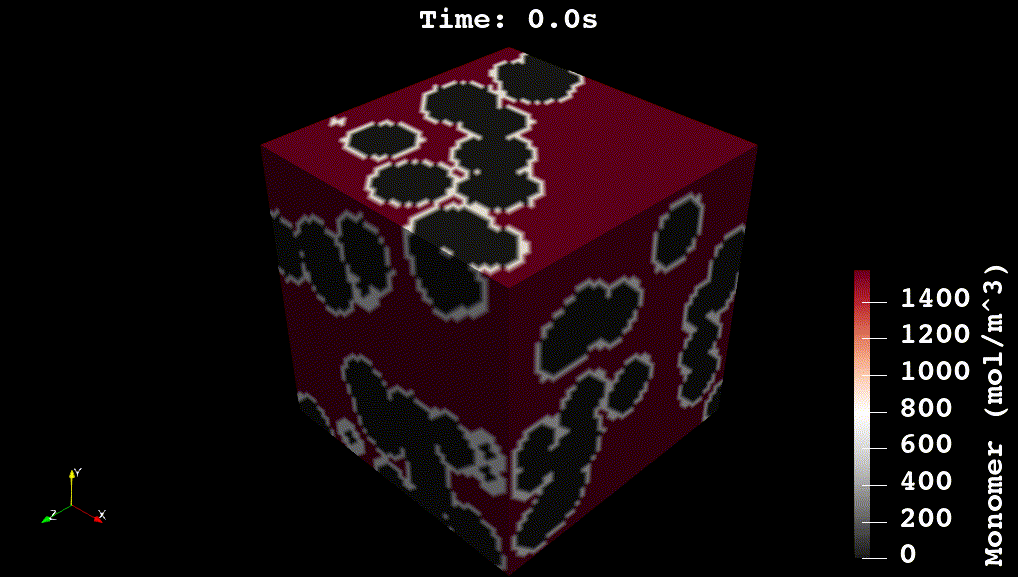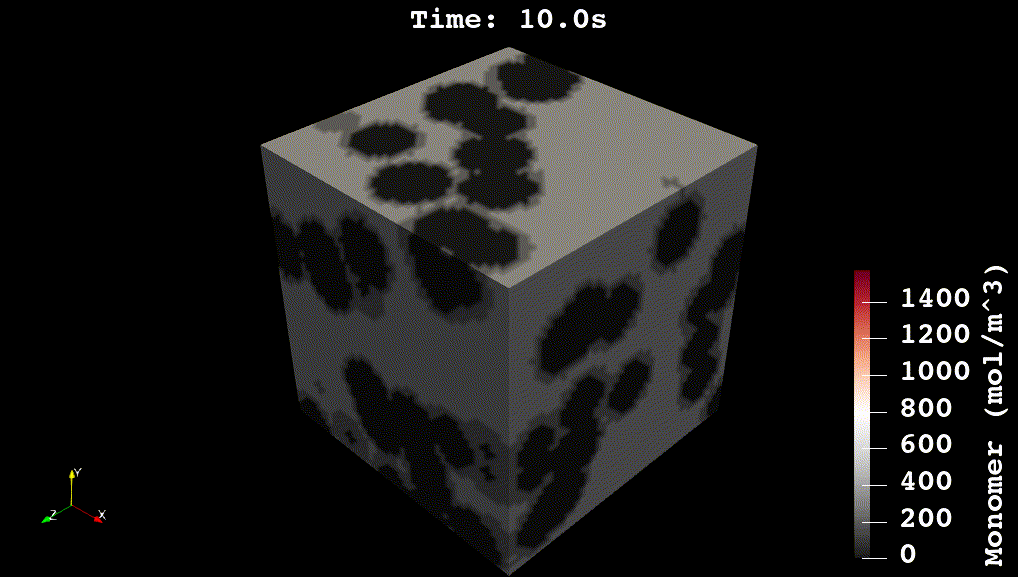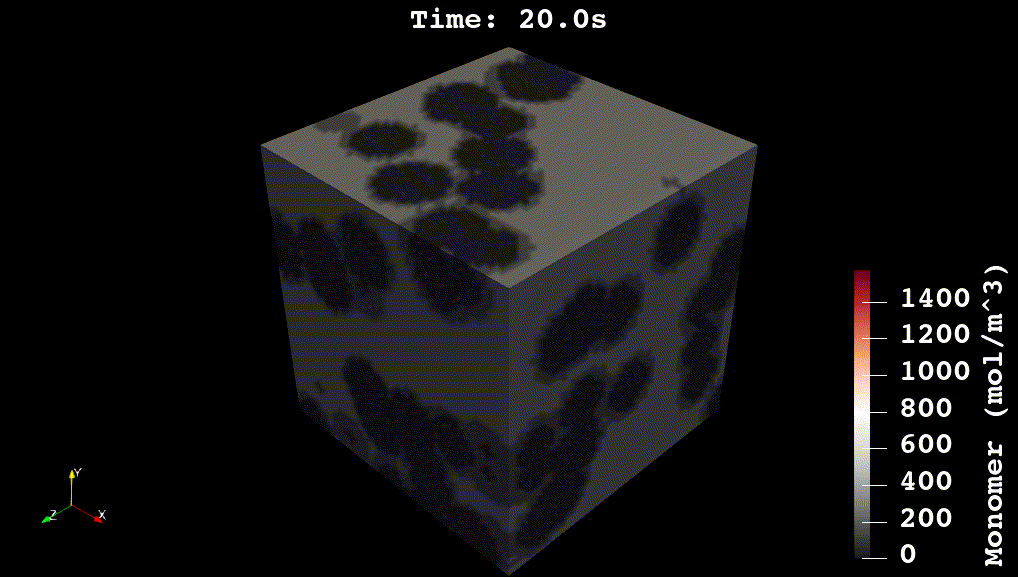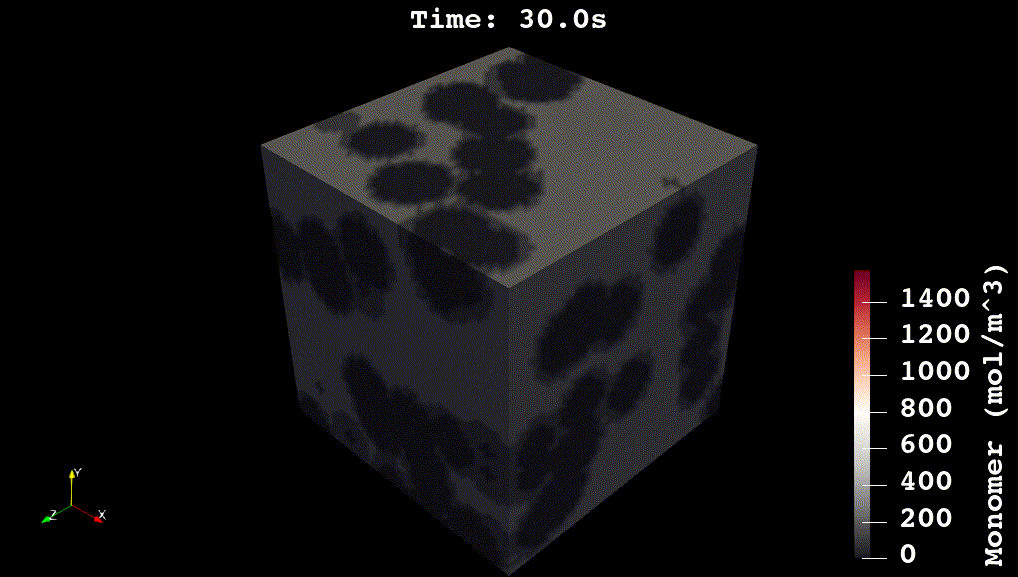
Reaction Kinetics for Advanced Materials
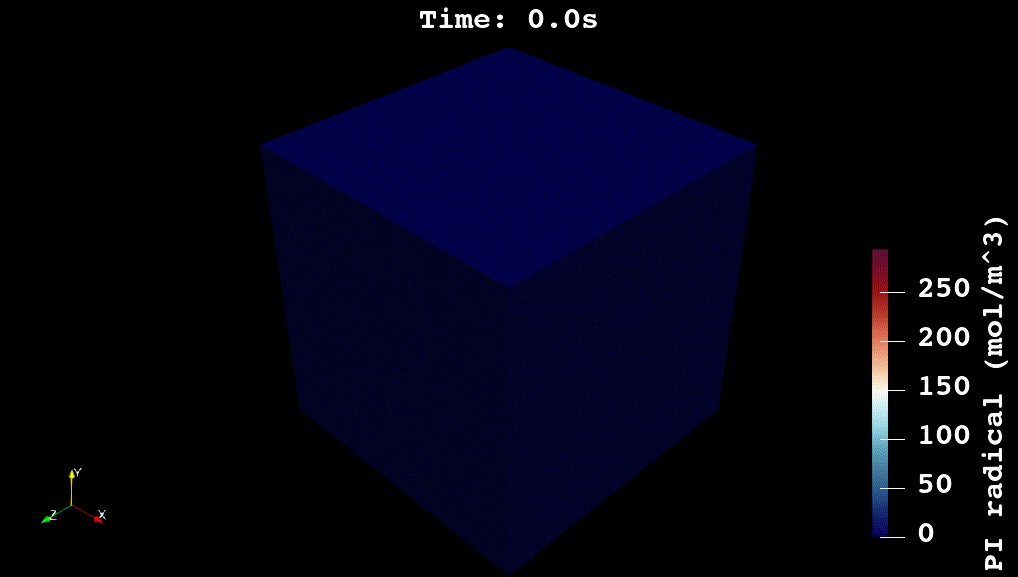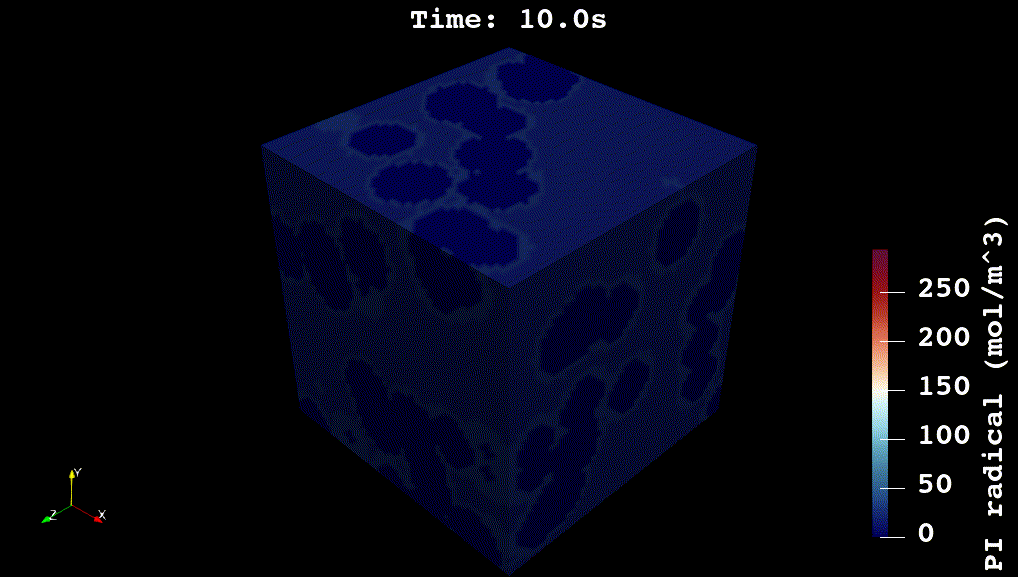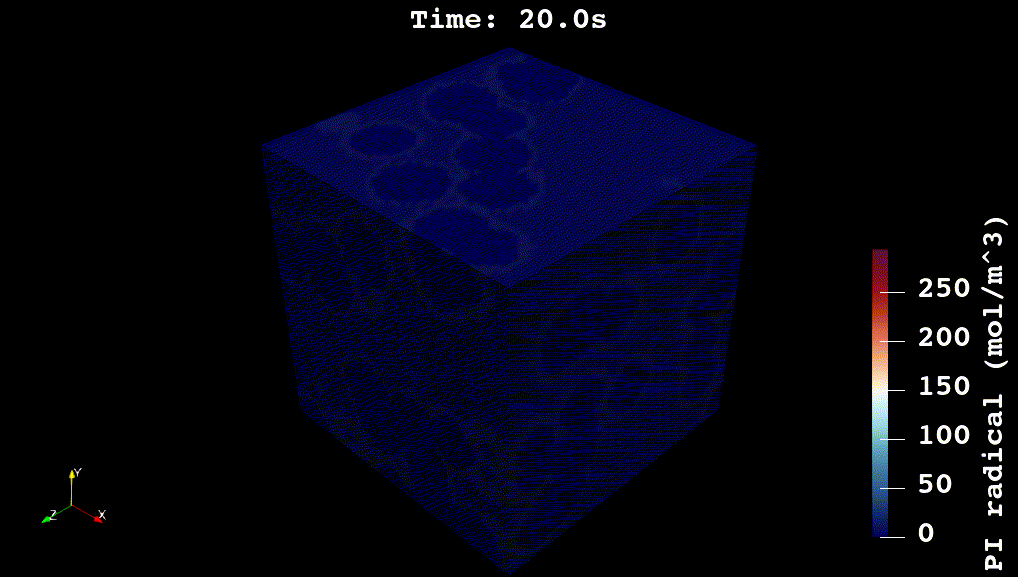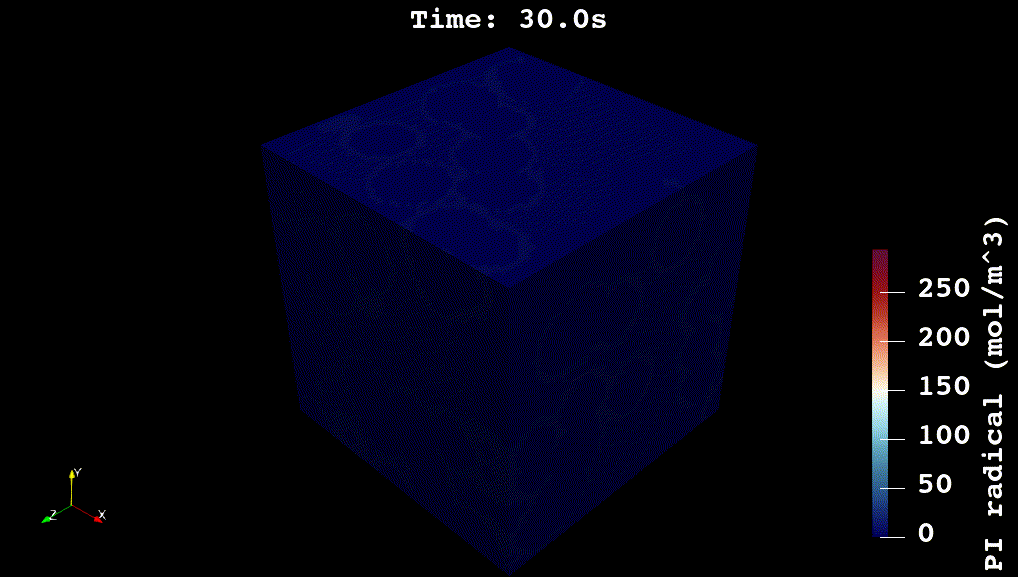
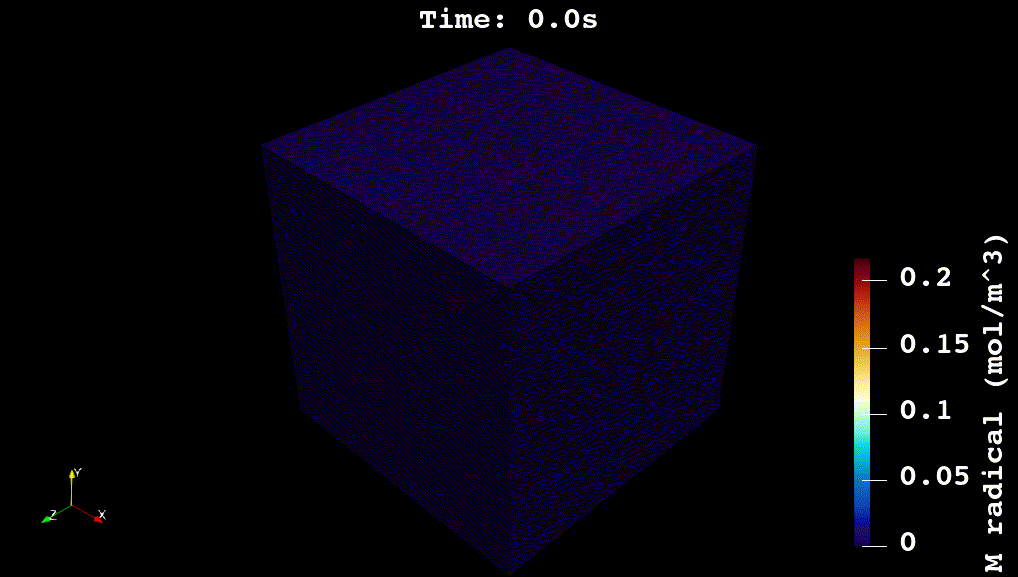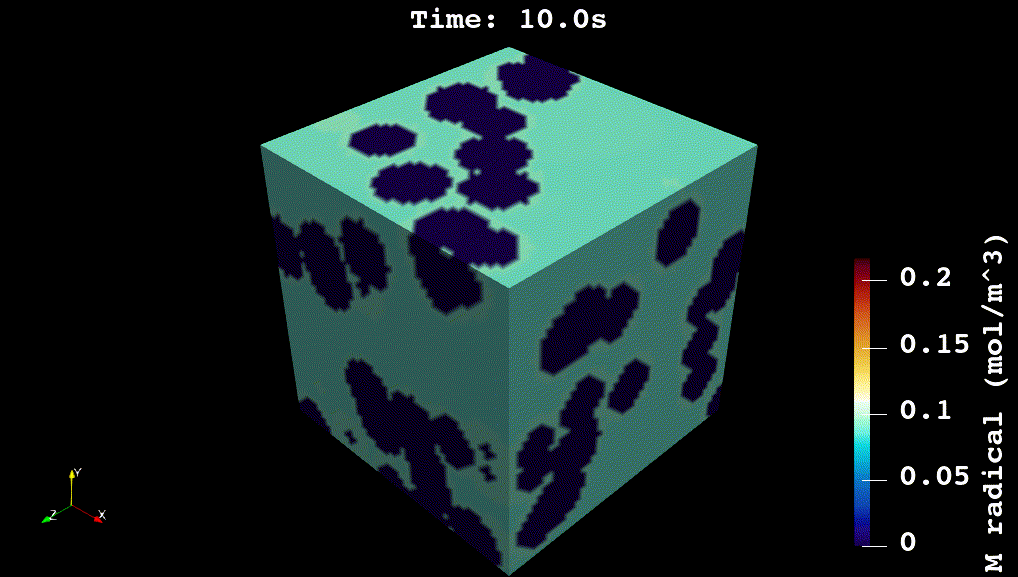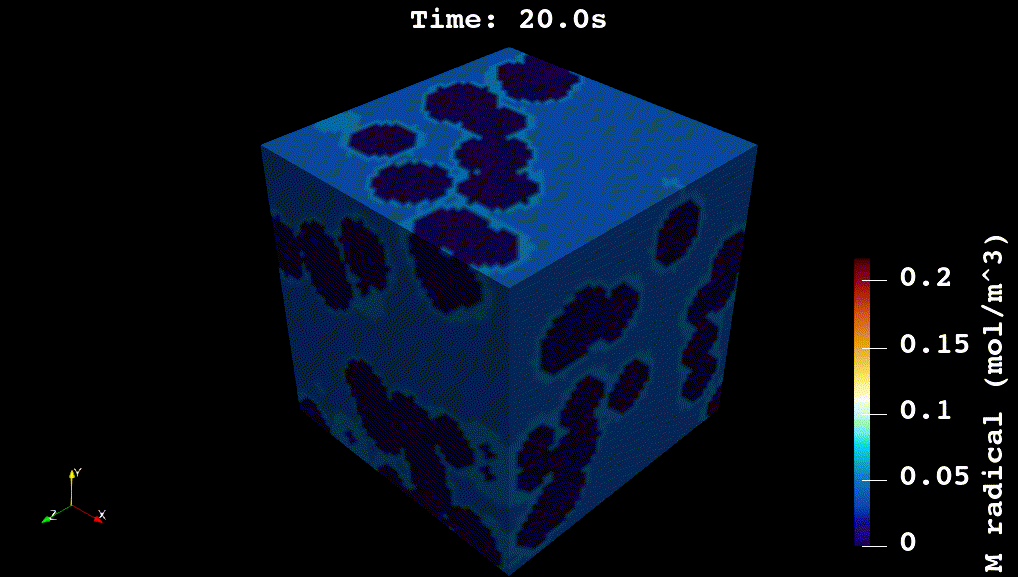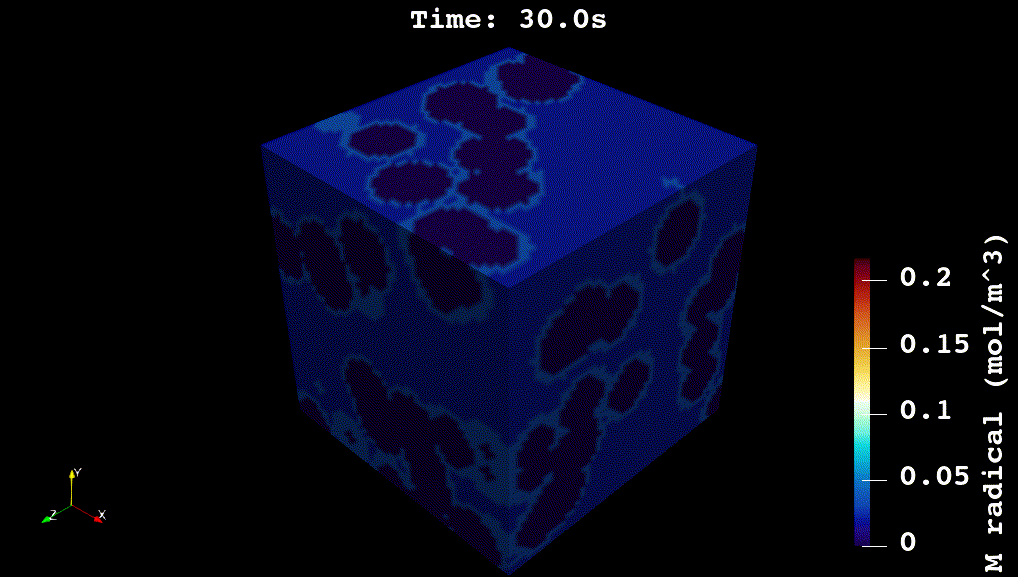
For my doctoral work, I worked on developing physics-based and machine learning models for reaction kinetics in advanced materials. The physics-based models were developed in C++ using voxel-computing methods, Gaussian Processes, and non-convex optimization methods (see Github code). The overall simulation solves a system of partial differential equations for reaction, diffusion, and heat transfer:
\(
\frac{\partial [PI]}{\partial t} = -\frac{\phi}{2} I_{abs}
\)
\(
\frac{\partial [PI\cdot]}{\partial t} =
\nabla_x \cdot \big(\kappa \nabla_x [PI\cdot]\big) + \phi I_{abs} - k_i [PI\cdot][M]
\)
\(
\frac{\partial [M_n \cdot]}{\partial t} =
\nabla \cdot \big(\kappa_{M_n \cdot} \nabla [M_n \cdot]\big) + k_i [PI\cdot][M] - k_t [M_n \cdot]^2
\)
\(
\frac{\partial [M]}{\partial t} =
\nabla_x \cdot \big(\kappa_M \nabla_x [M]\big) - k_i [PI\cdot][M] - k_p[M][M_n \cdot]
\)
\(
\rho C \frac{\partial \theta}{\partial t} =
\nabla_x \cdot \big(\kappa \nabla_x \theta\big)
+ \big(k_i [PI\cdot][M] + k_p[M][M_n \cdot] + k_t [M_n \cdot]^2\big) \Delta H
+ \epsilon I_0 e^{-\epsilon z}. \)
+ \big(k_i [PI\cdot][M] + k_p[M][M_n \cdot] + k_t [M_n \cdot]^2\big) \Delta H
+ \epsilon I_0 e^{-\epsilon z}. \)